Binary Tree

Definitions

In computer science, a binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.

Properties

1. The maximum number of nodes at level $i$ of a binary tree is $2^{i-1} (i \geqslant 1)$ or $2^i(i \geqslant 0)$.

Here level is the number of nodes on the path from the root to the node (including root and node). Level of the root is 1.

Proof: 

Let,  the maximum number of nodes on level i is S(i) = $2^{i-1}$ 

        S(1) = $2^{1-1}$ = $2^0$ = 1 (By substituting $i$ = 1 on both sides)

        $\therefore$ S(1) is true.

Let, S(i) be true for some natural number k.

i.e., S(k) = $2^{k-1}$  

Now,  

       Since in Binary tree every node has at most 2 children, next level (k+1) would have twice nodes.

i.e., S(k+1) = 2* S(k) = 2 * $2^{k-1}$ = $2^{(k-1)+1}$ = $2^k$ = $2^{(k+1)-1}$    

$\Longrightarrow$  S(k+1) is true.

Hence by principle of mathematical induction, the maximum number of nodes at level $i$ of a binary tree is $2^{i-1} (i \geqslant 1)$.

2. The maximum number of nodes in a binary tree of height $h$ is $ 2^h-1$ ($h \geqslant 1$) or $2^{h+1}-1(h \geqslant 0)$. 

Here the height of a tree is the maximum number of nodes on the root to leaf path. Height of a tree with a single node is considered as 1. 

This result can be derived from property 1 above.The maximum number of  nodes at level $i$ is $2^{i-1}$. The maximum number of  nodes at level $h$ is $2^{h-1}$.

A tree has maximum nodes if all levels have maximum nodes. So maximum number of nodes in a binary tree of height $h$ is $$2^0+2^1+2^2+..+2^{h-1} = \sum_{i=1}^h 2^{i-1} = 2^h-1$$.

Proof:

Let, $S_h = 2^0+2^1+2^2+..+2^{h-1} = 1+2+4+..+2^{h-1}$   ($h \geqslant 1$)  (2-1)

Multiply by 2 on both sides of the (1) equation.

i.e., $2 * S_h = 2+4+..+2^{h-1}+2^h$   (2-2)

Equation (2-2) minus equation (2-1) is as follows:

(2-2) - (2-1) = $2*S_h - S_h$ = $S_h$ = $2^h  - 1$

3. In binary tree the number of nodes with two children is exactly one less than the number of leaves(node without children).

Proof:

 

Assume the number of leaves is $n_0$, the number of nodes with one child is $n_1$ and the number of nodes with two children is $n_2$. The number of all nodes is $n$.

$n = n_0 + n_1 + n_2$    (3-1)

Look at the number of branches of the binary tree.

Except for the root node, all other nodes have a branch to enter, let $b$ be the total number of branches, then $n = b + 1$. 

Since these branches are come from nodes with one or two children. The number of branches of nodes with one child is $n_1$. The number of branches of nodes with two children is $2n_2$. So there is $b = n_1 + 2n_2$.

then:

$n =  n_1 + 2n_2 + 1$  (3-2)

Equation (3-1) minus equation (3-2) is as follows:

(3-1) - (3-2) $= n - n = 0 = n_0 - n_2 - 1$

$\therefore$ $n_0 = n_2 + 1$

Hence, in binary tree the number of nodes with two children is exactly one less than the number of leaves.

 

4.  In a binary tree with $N$ nodes, minimum possible height  is $Log_2(N+1)$ (The height of a root node is considered as 1).

Assume the height of binary tree with N nodes is h. 

 

$N \leqslant 2^h-1$  (Property 2 above)

$N ＋1 \leqslant 2^h$

Take the log of both sides of the inequality .

$log_2{(N + 1)} \leqslant h $

$h \geqslant log_2{(N + 1)}$ 

Hence proved. 

5. A binary tree with $L$ leaves has at least $\lfloor log_2L \rfloor$+ 1 levels

proof:

A binary tree has the maximum number of leaves (and a minimum number of levels) when all levels are fully filled. Let all leaves be at level $l$, then below is true for the number of leaves L.

$L \leqslant 2^{l-1}$  (Property 1 above)

Take the log of both sides of the inequality .

$log_2L \leqslant l - 1$

$log_2L + 1 \leqslant l$

$l = \lfloor log_2L \rfloor + 1$

Where $l$ is the minimum number of levels.

Hence proved.

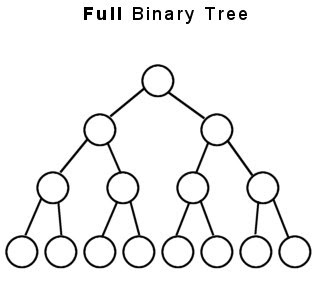
Full Binary Tree and Complete Binary Tree

A binary Tree is a full binary tree if every node has 0 or 2 children. The full binary trees as following:

or

A complete binary tree is binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. A complete binary tree as following:

 

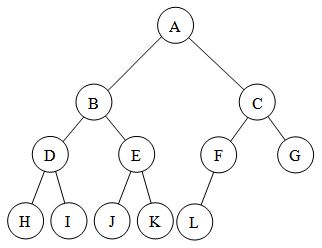
6. The height of a complete binary tree with $n$ nodes is $\lfloor log_2n \rfloor + 1$

proof:

 

Assume the height of the complete binary tree is $h (h \geqslant 1)$. The number of the complete binary tree is n.

$n \leqslant  2^h - 1$   (This can be directly derived from property 2 above.)

And 

$2^{h-1} - 1 < n $ (At least one node is at level h.)

so there is:

$2^{h-1} - 1 < n \leqslant 2^h - 1$

The maximum number of nodes in a binary tree of height $h-1$ is $2^{h-1}-1$. A complete binary tree of height $h$ has at least one more node than $2^{h-1}-1$, and it is $2^{h-1}$.

So there is $2^{h-1} \leqslant n$.

The maximum number of nodes in a binary tree of height $h$ is $2^h-1$. A complete binary tree of height $h+1$ has at least one more node than $2^h-1$, and it is $2^{h}$.

So there is $n < 2^h$.

$\therefore$ $2^{h-1} \leqslant n < 2^h$

Taking log on both sides of the inequality above:

$h-1 \leqslant log_2n < h$ 

The height of the complete binary tree $h$ must be an integer, but $log_2n$ may not be an integer. So we take the lower integer:

$h-1 = \lfloor log_2n \rfloor $ 

$h = \lfloor log_2n \rfloor + 1$

 

Hence proved.

References:

Binary Tree | Set 2 (Properties)

Proof of Sum of a Geometric Series - Corbettmaths

数据结构(严蔚敏)

 

${\displaystyle 2^{h+1}-1}$