Binary Search Trees
What is a binary search tree?
A binary search tree is organized, as the name suggests, in a binary tree, as following:
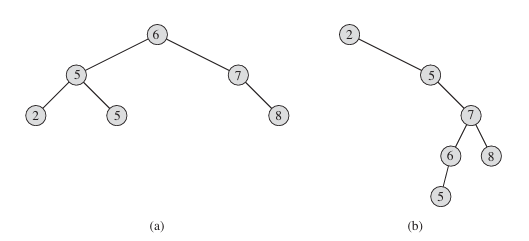
Figure 1 Binary search trees. For any node x, the keys in the left subtree of x are at most x: key, and the keys in the right subtree of x are at least x: key. Different binary search trees can represent the same set of values. The worst-case running time for most search-tree operations is proportional to the height of the tree. (a) A binary search tree on 6 nodes with height 2. (b) A less efficient binary search tree with height 4 that contains the same keys.
We can represent such a tree by a linked data structure in which each node is an object. In addition to a key and satellite data, each node contains attributes left, right and p that point to the nodes corresponding to its left child, its right child, and its parent, respectively. If a child or the parent is missing, the appropriate attribute contains the value NIL. The root node is the only node in the tree whose parent is NIL.
The keys in a binary search tree are always stored in such a way as to satisfy the binary-search-tree property:
Let x a node in a binary search tree. If y is a node in the left subtree of x, then y.key <= x.key. If y is a node in the right subtree of x, then y.key >= x.key.
Thus, in Figure 1(a), the key of the root is 6, the keys 2, 5, and 5 in its left subtree are no larger than 6, and the keys 7 and 8 in its right subtree are no smaller than 6. The same property holds for every node in the tree. For example, the key 5 in the root’s left child is no smaller than the key 2 in that node’s left subtree and no larger than the key 5 in the right subtree.
The binary-search-tree property allows us to print out all the keys in a binary search tree in sorted order by a simple recursive algorithm, called an inorder tree walk. This algorithm is so named because it prints the key of the root of a subtree between printing the values in its left subtree and printing those in its right subtree. (Similarly, a preorder tree walk prints the root before the values in either subtree, and a postorder tree walk prints the root after the values in its subtrees.) To use the following procedure to print all the elements in a binary search tree T , we call INORDER-TREE-WALK(T.root).
if x != NIL
INORDER-TREE-WALK(x.left)
print x.key
INORDER-TREE-WALK(x.right)
As an example, the inorder tree walk prints the keys in each of the two binary search trees from Figure 1 in the order 2, 5, 5, 6, 7, 8. The correctness of the algorithm follows by induction directly from the binary-search-tree property.
It takes $\Theta$(n) time to walk an n-node binary search tree, since after the initial call, the procedure calls itself recursively exactly twice for each node in the tree, once for its left child and once for its right child. The following theorem gives a formal proof that it takes linear time to perform an inorder tree walk.
Proof
Let T(n) denote the time taken by INORDER-TREE-WALK when it is called on the root of an n-node subtree. Since INORDER-TREE-WALK visits all n nodes of the subtree, we have T(n) = $\Omega$(n). It remains to show that T(n) = O(n).
Since INORDER-TREE-WALK takes a small, constant amount of time on an empty subtree (for the test x != NIL), we have T(0) = c for some constant c > 0.
For n > 0, suppose that INORDER-TREE-WALK is called on a node x whose left subtree has k nodes and whose right subtree has n - k -1 nodes. The time to perform INORDER-TREE-WALK(x) is bounded by T(n) <= T(k) + T(n-k-1) + d from some constant d > 0 that reflects an upper bound on the time to execute the body of INORDER-TREE-WALK(x), exclusive of the time spent in recursive calls.
We use the substitution method to show that T(n) = O(n) by proving that T(n) <= (c + d)n + c . For n = 0, we have (c + d)*0 + c = c = T(0). For n > 0, we have
T(n) <= T(k) + T(n - k - 1) + d
= ((c + d)k + c) + ((c+d)(n - k - 1) + c) + d
= (c + d)n + c - (c+d) + c + d
= (c + d)n + c,
which completes the proof.
Querying a binary search tree
We often need to search for a key stored in a binary search tree. Besides the search operation, binary search trees can support such queries as MINIMUM, MAXIMUM, SUCCESSOR, and PREDECESSOR.
Searching
We use the following procedure to search for a node with a given key in a binary search tree. Given a pointer to the root of the tree and a key k, TREE-SERACH return a pointer to a node with key k if one exists; otherwise, it returns NIL.
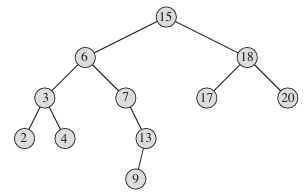
Figure 2 Queries on a binary search tree. To search for the key 13 in the tree, we follow the path 15 -> 6 -> 7 -> 13 from the root. The minimum key in the tree is 2, which is found by following left pointers from the root. The maximum key 20 is found by following right pointers from the root. The successor of the node with key 15 is the node with key 17, since it is the minimum key in the right subtree of 15. The node with key 13 has no right subtree, and thus its successor is its lowest ancestor whose left child is also an ancestor. In this case, the node with key 15 is its successor.
if x == NIL or k == x.key
return x
if k < x.key
return TREE-SEARCH(x.left, k)
else return TREE-SEARCH(x.right, k)
The nodes encountered during the recursion form a simple path downward from the root of the tree, and thus the running time of TREE-SEARCH is O(h), where h is the height of the tree.
We can rewrite this procedure in an iterative fashion by “unrolling” the recursion into a while loop. On most computers, the iterative version is more efficient.
while x != NIL and k != x.key
if k < x.key
x = x.left
else x = x.right
return x
Minimum and maximum
We can always find an element in a binary search tree whose key is a minimum by following left child pointers from the root until we encounter a NIL, as shown in Figure 2. The following procedure returns a pointer to the minimum element in the subtree rooted at a given node x, which we assume to be non-NIL:
while x.left != NIL
x = x.left
return x
The binary-search-tree property guarantees that TREE-MINIMUM is correct. If a node x has no left subtree, then since every key in the right subtree of x is at least as large as x.key, the minimum key in the subtree rooted at x is x.key. If node x has a left subtree, then since no key in the right subtree is smaller than x.key and every key in the left subtree is not larger than x.key, the minimum key in the subtree rooted at x resides in the subtree rooted at x.left.
The pseudocode for TREE-MAXIMUM is symmetric:
while x.right != NIL
x = x.right
return x
Both of these procedures run in O(h) time on a tree of height h since, as in TREE-SEARCH, the sequence of nodes encountered forms a simple path downward from the root.
Successor and predecessor
Given a node in a binary search tree, sometimes we need to find its successor in the sorted order determined by an inorder tree walk. If all keys are distinct, the successor of a node x is the node with the smallest key greater than x.key. The structure of a binary search tree allows us to determine the successor of a node without ever comparing keys. The following procedure returns the successor of a node x in a binary search tree if it exists, and NIL if x has the largest key in the tree:
if x.right != NIL
return TREE-MINIMUM(x.right)
y = x.p
while y != NIL and x == y.right
x = y
y = y.p
return y
We break the code for TREE-SUCCESSOR into two cases. If the right subtree of node x is nonempty, then the successor of x is just the leftmost node in x's right subtree, which we find in line 2 by calling TREE-MINIMUM(x.right). For example, the successor of the node with key 15 in Figure 2 is the node with key 17.
On the other hand, if the right subtree of node x is empty and x has a successor y, then y is the lowest ancestor of x whose left child is also an ancestor of x. In figure 2, the successor of the node with key 13 is the node with key 15. To find y, we simply go up the tree from x until we encounter a node that is the left child of its parent; line 3-7 of TREE-SUCCESSOR handle this case.
The running time of TREE-SUCCESSOR on a tree of height h is O(h), since we either follow a simple path up the tree or follow a simple path down the tree. The procedure TREE-PREDECESSOR, which is symmetric to TREE-SUCCESSOR, also runs in time O(h).
Even if keys are not distinct, we define the successor and predecessor of anynode x as the node returned by calls made to TREE-SUCCESSOR(x) and TREE-PREDECESSOR(x), respectively.
In summary, we have proved the following theorem.
Insertion and deletion
The operations of insertion and deletion cause the dynamic set represented by a binary search tree to change. The data structure must be modified to reflect this change, but in such a way that the binary-search-tree property continues to hold. As we shall see, modifying the tree to insert a new element is relatively straight-forward, but handling deletion is somewhat more intricate.
Insertion
To insert a new value v into a binary search tree T, we use the procedure TREE-INSERT. The procedure takes a node z for which z.key = v, z.left = NIL, and z.right = NIL. It modifies T and some of the attributes of z in such a way that it inserts z into an appropriate position in the tree.
TREE-INSERT(T, z)
y = NIL
x = T.root
while x != NIL
y = x
if z.key < x.key
x = x.left
else x = x.right
z.p = y
if y == NIL
T.root = z // tree T was empty
elseif z.key < y.key
y.left = z
else y.right = z
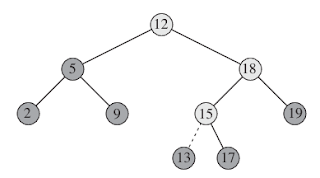
Figure 3 Inserting an item with key 13 into a binary search tree. Lightly shaded nodes indicate the simple path from the root down to the position where the item is inserted. The dashed line indicates the link in the tree that is added to insert the item.
Figure 3 shows how TREE-INSERT works. Just like the procedures TREE-SEARCH and ITERATIVE-TREE-SEARCH, TREE-INSERT begins at the root of the tree and the pointer x traces a simple path downward looking for a NIL to replace with the input item z. The procedure maintains the trailing pointer y as the parent of x. After initialization, the while loop in lines 3–7 causes these two pointers to move down the tree, going left or right depending on the comparison of z.key with x.key, until x becomes NIL. This NIL occupies the position where we wish to place the input item z. We need the trailing pointer y, because by the time we find the NIL where z belongs, the search has proceeded one step beyond the node that needs to be changed. Lines 8–13 set the pointers that cause z to be inserted.
Like the other primitive operations on search trees, the procedure TREE-INSERT runs in O(h) time on a tree of height h.
Deletion
The overall strategy for deleting a node z from a binary search tree T has three basic cases but, as well as shall see, one of the cases is a bit tricky.
- If z has no children, then we simply remove it by modifying its parent to replace z with NIL as its child.
- If z has just one child, then we elevate that child to take z's position in the tree by modifying z's parent to replace z by z's child.
- If z has two children, then we find z's successor y -- which must be in z's right subtree -- and have y take z's position in the tree. The rest of z's original right subtree becomes y's new right subtree, and z's left subtree becomes y's new left subtree. This case is the tricky one because, as we shall see, it matters whether y is z's right child.
The procedure for deleting a given node z from a binary search tree T takes as arguments pointers to T and z. It organizes its cases a bit differently from the three cases outlined previously by considering the four cases shown in Figure 4.
- If z has no left child (part (a) of the figure), then we replace z by its right child, which may or may not be NIL. When z's right child is NIL, this case deals with the situation in which z has no children. When z's right child is non-NIL, this case handles the situation in which z has just one child, which is its right child.
- If z has just one child, which is its left child (part (b) of the figure), then we replace z by its left child.
- Otherwise, z has both a left and a right child. We find z's successor y, which lies in z's right subtree and has no left child. We want to splice y out of its current location and have it replace z in the tree.
- If y is z's right child (part (c)), then we replace z by y, leaving y's right child alone.
- Otherwise, y lies within z's right subtree but is not z's right child (part (d)). In this case, we first replace y by its own right child, and then we replace z by y.
In order to move subtrees around within the binary search tree, we define a subroutine TRANSPLANT, which replaces one subtree as a child of its parent with another subtree. When TRANSPLANT replaces the subtree rooted at node u with the subtree rooted at node v, node u's parents becomes node v's parent, and u's parent ends up having v as its appropriate child.
if u.p == NIL
T.root = v
elseif u == u.p.left
u.p.left = v
else u.p.right = v
if v != NIL
v.p = u.p
Lines 1-2 handle the case in which u is the root of T. Otherwise, u is either a left child or a right child of its parent. Lines 3-4 take care of updating u.p.left if u is a left child, and line 5 updates u.p.right if u is a right child. We allow v to be NIL, and lines 6-7 update v.p if v is non-NIL. Note the TRANSPLANT does not attempt to update v.left and v.right; doing so, or not doing so, is the responsibility of TRANSPLANT's caller.
With the TRANSPLANT procedure in hand, here is the procedure that deletes node z from binary search tree T:
if z.left == NIL
TRANSPLANT(T, z, z.right)
elseif z.right == NIL
TRANSPLANT(T, z, z.left)
else y = TREE-MINIMUM(z.right)
if y.p != z
TRANSPLANT(T, y, y.right)
y.right = z.right
y.right.p = y
TRANSPLANT(T, z, y)
y.left = z.left
y.left.p = y
The TREE-DELETE procedure executes the four cases as follows. Lines 1-2 handle the case in which node z has no left child, and lines 3-4 handle the case in which z has a left child but no right child. Lines 5-12 deal with the remaining two cases, in which z has two children. Line 5 finds node y, which is the successor of z. Because z has a nonempty right subtree, its successor must be the node in that subtree with the smallest key; hence the call to TREE-MINIMUM(z.right). As we noted before, y has no left child. We want to splice y out of its current location, and it should replace z in the tree. If y is z's right child, then lines 10-12 replace z as a child of its parent by y and replace y's left child by z's left child. If y is not z's left child, lines 7-9 replace y as a child of its parent by y's right child and turn z's right child into y's right child, and then lines 10-12 replace z as a child of its parent by y and replace y's left child by z's left child.
Each line of TREE-DELETE, including the calls to TRANSPLANT, takes constant time, except for the call to TREE-MINIMUM in line 5. Thus, TREE-DELETE runs in O(h) time on tree of height h.
In summary, we have proved the following theorem.
References:
Introduction to algorithms


Comments
Post a Comment