Red-Black Trees
Binary Search Trees showed that a binary search tree of height h can support any of the basic dynamic-set operations—such as SEARCH, PREDECESSOR, SUCCESSOR, MINIMUM, MAXIMUM, INSERT, and DELETE—in O(h) time. Thus, the set operations are fast if the height of the search tree is small. If its height is large, however, the set operations may run no faster than with a linked list. Red-black trees are one of many search-tree schemes that are “balanced” in order to guarantee that basic dynamic-set operations take O($log_2n$) time in the worst case.
Properties of red-black trees
A red-black tree is a binary search tree with one extra bit of storage per node; its color, which can be either RED or BLACK. By constraining the node colors on any simple path from the root to a leaf, red-black trees ensure that no such path is more than twice as long as any other, so that the tree is approximately balanced.
Each node of the tree now contains the attribute color, key, left, right, and p. If a child or the parent of a node does not exist, the corresponding pointer attribute of the node contains the value NIL. We shall regard these NILs as being pointers to leaves (external nodes) of the binary search tree and the normal, key-bearing nodes as being internal nodes of the tree.
A red-black tree is a binary tree that satisfies the following red-black properties:
- Every node is either red or black.
- The root is black.
- Every leaf (NIL) is black.
- If a node is red, then both its children are black.
- For each node, all simple paths from the node to descendant leaves contains the same number of black nodes.
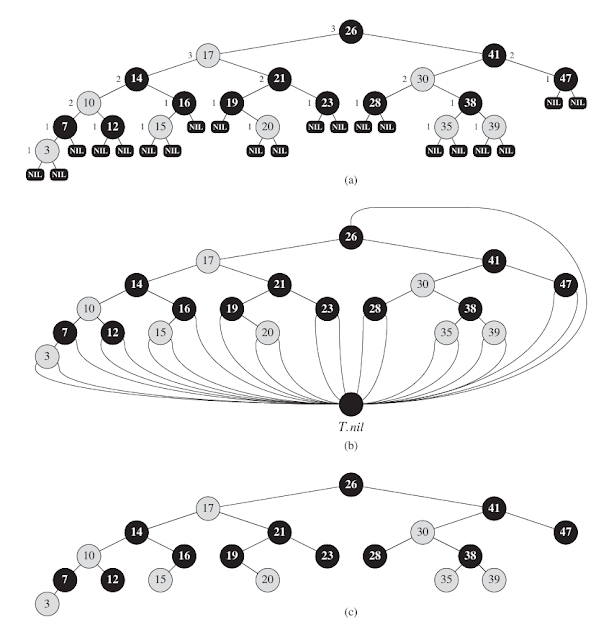
Figure 1(a) show an example of a red-black tree.
As a matter of convenience in dealing with boundary conditions in red-black tree code, we use a single sentinel to represent NIL. For a red-black tree T, the sentinel T.nil is an object with the same attributes as an ordinary node in the tree. Its color attribute is BLACK, and its other attributes --p, left, right and key -- can take on arbitrary values. As figure 1(b) shows, all pointers to NIL are replaced by pointers to the sentinel T.nil.
We use the sentinel so that we can treat a NIL child of a node x as an ordinary node whose parent is x. Although we instead could add a distinct sentinel node for each NIL in the tree, so that the parent of each NIL is well defined, that approach would waste space. Instead, we use the one sentinel T.nil to represent all the NILs -- all leaves and the root's parent. The values of attributes p, left, right and key of the sentinel are immaterial, although we may set them during the course of a procedure for our convenience.
We generally confine our interest to the internal nodes of a red-black tree, since they hold the key values. In the remainder of this article, we omit the leaves when we draw red-black trees, as show in figure 1(c).
We call the number of black nodes on any simple path from, but not including, a node x down to a leaf the black-height of the node, denoted bh(x). By property 5, the notion of black-height is well defined, since all descending simple path from the node have the same number of black nodes. We define the black-height of a red-black tree to be the black-height of its root.
The following lemma shows why red-black trees make good search trees.
Proof We start by showing that the subtree rooted at any node x contains at least $2^{bh(x)}-1$ internal nodes. We prove this claim by induction on the height of x. If the height of x is 0, then x must be a leaf (T.nil), and the subtree rooted at x indeed contains at least $2^{bh(x)}-1 = 2^0 - 1 = 0$ internal nodes. For the inductive step, consider a node x that has positive height and is and internal node with two children. Each child has a black-height of either bh(x) or bh(x) - 1, depending on whether its color is red or black, respectively. Since the height of a child of x is less than the height of x itself, we can apply the inductive hypothesis to conclude that each child has at least $2^{bh(x)-1}-1$ internal nodes. Thus, the subtree rooted at x contains at least ($2^{bh(x)-1}-1$) + ($2^{bh(x)-1}-1$) + 1 = $2^{bh(x)}-1$ internal nodes, which proves the claim.
To complete the proof of the lemma, let h be the height of the tree. According to property 4, at least half the nodes on any simple path from the root a leaf, not including the root, must be black. Consequently, the black-height of the root must be at least $\frac{h}{2}$; thus, $n >= 2^{\frac{h}{2}}-1$ .
Moving the 1 to the left hand side and taking logarithms on both sides yields $log_2{(n+1)} >= \frac{h}{2}$, or $h <= 2log_2{(n+1)}$.
As an immediate consequence of this lemma, we can implement the dynamic-set operations SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, and PREDECESSOR in O($log_2n$) time on red-black trees, since each can run in O(h) time on a binary search tree of height h and any red-black tree on n nodes is a binary search tree with height O($log_2n$).
Rotations
The search-tree operations TREE-INSERT and TREE-DELETE, when run on a red-black tree with n keys, take O($log_2n$) time. Because they modify the tree, the result may violate the red-black properties enumerated above. To restore these properties, we must change the colors of some the nodes in the tree and also change the pointer structure.
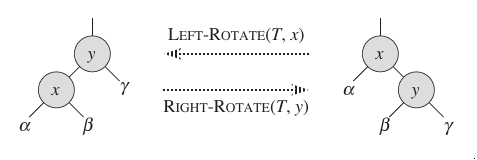
We change the pointer structure through rotation, which is a local operation in a search tree that preserves the binary-search-tree property. Figure 2 shows the two kinds of rotation: left rotations and right rotations. When we do a left rotation on a node x, we assume that its right child y is not T.nil; x may be any node in the tree whose right child is not T.nil. The left rotation "pivots" around the link from x to y. It makes y the new root of the subtree, with x as y's left child and y's left child as x's right child.
The pseudocode for LEFT-ROTATE assumes that x.right != T.nil and that the root's parent is T.nil.
LEFT-ROTATE(T, x)
y = x.right // set y
x.right = y.left // turn y's left subtree into x's right subtree
if y.left != T.nil
y.left.p = x
y.p = x.p // link x's parent to y
if x.p == T.nil
T.root = y
elseif x == x.p.left
x.p.left = y
else x.p.right = y
y.left = x // put x on y's left
x.p = y
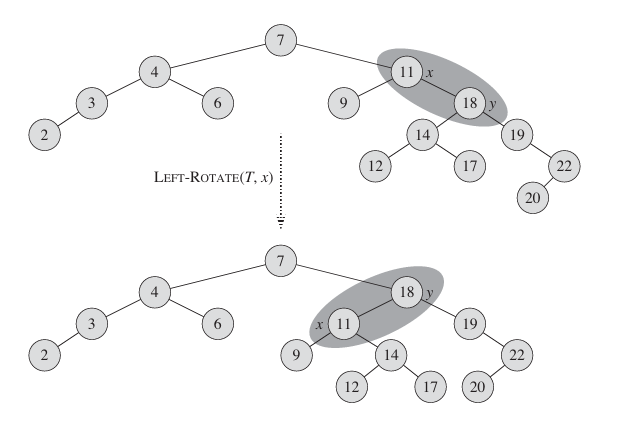
Figure 3 shows an example of how LEFT-ROTATE modifies a binary search tree. The code for RIGHT-ROTATE is symmetric. Both LEFT-ROATE and RIGHT-ROTATE run in O(1) time. Only pointers are changed by a rotation; all other attributes in a node remain the same.
Figure 3 An example of how the procedure LEFT-ROTATE(T, x) modifies a binary search tree. Inorder tree walks of the input tree and the modified tree produce the same listing of key values.
RIGHT-ROTATE(T, y)
x = y.left // set x
y.left = x.right // turn x's right subtree into y's left subtree
if x.right != t.nil
x.right.p = y
x.p = y.p // link y's parent to x
if y.p == t.nil
t.root = x
elseif y == y.p.left
y.p.left = x
else y.p.right = x
x.right = y // put y on x's right
y.p = x
Insertion
We can insert a node into an n-node red-black tree in O($log_2n$) time. To do so, we use a slightly modified version of the TREE-INSERT procedure (binary search trees) to inserted node z into the tree T as if it were an ordinary search tree, and then we color z red. To guarantee that the red-black properties are preserved, we then call an auxiliary procedure RB-INSERT-FIXUP to recolor nodes and perform rotations. The call RB-INSERT(T, z) inserts node z, whose key is assumed to have already been filled in, into the red-black tree T.
RB-INSERT(T, z)
y = T.nil
x = T.root
while x != T.nil
y = x
if z.key < x.key
x = x.left
else x = x.right
z.p = y
if y == T.nil
T.root = z
elseif z.key < y.key
y.left = z
else y.right = z
z.left = T.nil
z.right = T.nil
z.color = RED
RB-INSERT-FIXUP(T, z)
The procedures TREE-INSERT and RB-INSERT differ in four ways. First, all instance of NIL in TREE-INSERT are replaced by T.nil. Second, we set z.left and z.right to T.nil in lines 14-15 of RB-INSERT, in order to maintain the proper tree structure. Third, we color z red in line 16. Fourth, because coloring z red may cause a violation of one of the red-black properties, we call RB-INSERT-FIXUP(T, z) in line 17 of RB-INSERT to restore the red-black properties.
RB-INSERT-FIXUP(T, z)
while z.p.color == RED
if z.p == z.p.p.left
y = z.p.p.right
if y.color == RED
z.p.color = BLACK // case 1
y.color = BLACK // case 1
z.p.p.color = RED // case 1
z = z.p.p // case 1
else // y(z's uncle) is not RED
if z == z.p.right // case 2
z = z.p // case 2
LEFT-ROTATE(T, z) // case 2
z.p.color = BLACK // case 3
z.p.p.color = RED // case 3
RIGHT-ROTATE(T, z.p.p) // case 3
else // z.p == z.p.p.right
y = z.p.p.left
if y.color == RED
z.p.color = BLACK // case 1
y.color = BLACK // case 1
z.p.p.color = RED // case 1
z = z.p.p // case 1
else // y(z's uncle) is not RED
if z == z.p.left // case 2
z = z.p // case 2
RIGHT-ROTATE(T, z) // case 2
z.p.color = BLACK // case 3
z.p.p.color = RED // case 3
LEFT-ROTATE(T, z.p.p) // case 3
T.root.color = BLACK
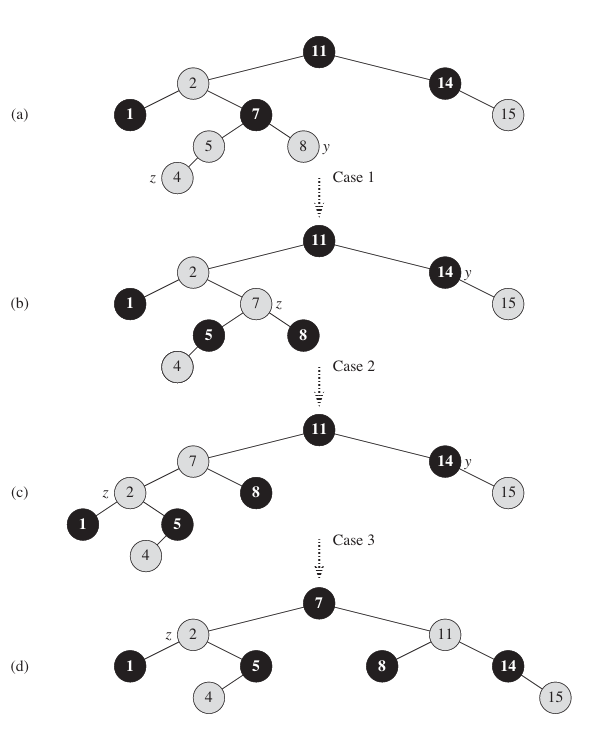
To understand how RB-INSERT-FIXUP works, we shall break out examination of the code into three major steps. First, we shall determine what violations of the red-black properties are introduced in RB-INSERT when node z is inserted and colored red. Second, we shall examine the overall goal of the while loop in lines 1-29. Finally, we shall explore each of the three cases within the while loop's body and see how the accomplish the goal. Figure 4 shows how RB-INSERT-FIXUP operates on a sample red-black tree.
Which of the red-black properties might be violated upon the call to RB-INSERT-FIXUP? Property 1 certainly continues to hold, as does property 3, since both children of the newly inserted red node are the sentinel T.nil. Property 5, which says that the number of black nodes is the same on every simple path from a given node, is satisfied as well, because node z replaces the (black) sentinel, and node z is red with sentinel children. Thus, the only properties that might be violated are property 2, which requires the root to be black, and property 4, which says that a red node cannot have a red child. Both possible violations are due to z being red. Property 2 is violated if z is the root, and property 4 is violated if z's parent is red. Figure 4(a) shows a violation of property 4 after the node z has been inserted.
The while loop in lines 1-29 maintains the following three-part invariant at the start of each iteration of the loop:
b. If z.p is the root, then z.p is black.
c. If the tree violates any of the red-black properties, then it violates at most one of them, and the violation is of either property 2 or property 4. If the tree violates property 2, it is because z is the root and is red. If the tree violates property 4, it is because both z and z.p are red.
Part (c), which deals with violations of red-black properites, is more central to showing that RB-INSERT-FIXUP restores the red-black properties than parts (a) and (b), which we use along the way to understand situations in the code. Because we'll be focusing on node z and nodes near it in the tree, it helps to know from part (a) that z is red. We shall use part (b) show that the node z.p.p exists when we reference it it lines 2, 3, 7, 8, 14, 15, 17, 21, 22, 28 and 29.
Recall that we need to show that a loop invariant is true prior to the first iteration of the loop, that each iteration maintains the loop invariant, and that the loop invariant gives us a useful property at loop termination.
We start with the initialization and termination arguments. Then, as we examine how the body of the loop works in more detail, we shall argue that the loop maintains the invariant upon each iteration. Along the way, we shall also demonstrate that each iteration of the loop has two possible outcomes: either the pointer z moves up the tree, or we perform some rotations and then the loop terminates.
Initialization: Prior to the first iteration of the loop, we start with a red-black tree with no violations, and we added a red node z. We show that each part of the invariant holds at the time RB-INSERT-FIXUP is called:
a. When RB-INSERT-FIXUP is called, z is the red node that was added.b. If z.p is the root, then z.p started out black and did not change prior to the call of RB-INSERT-FIXUP
c. We have already seen that properties 1, 3, and 5 hold when RB-INSERT-FIXUP is called.
If the tree violates property 4, then, because the children of node z are black sentinals and the tree had no other violations prior to z being added, the violation must be because both z and z.p are red. Moreover, the tree violates no other red-black properties.
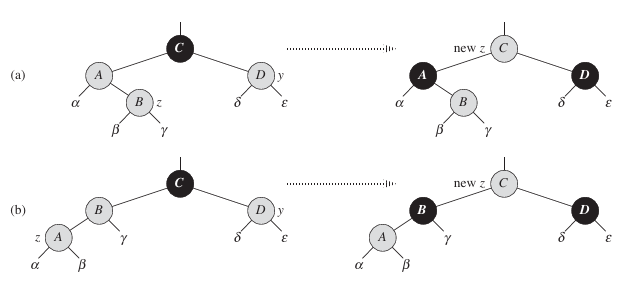
Figure 5 shows the situation for case 1 (lines 5-8), which occurs when both z.p and y are red. Because z.p.p is black, we can color both z.p and y black, thereby fixing the problem of z and z.p both being red, and we can color z.p.p red, thereby maintaining property 5. We then repeat the while loop with z.p.p as the new node z. The pointer z moves up two levels in the tree.
Now, we show that case 1 maintains the loop invariant at the start of the next iteration. We use z to denote node z in the current iteration, and $z'$ = z.p.p to denote the node that will be called node z at the test in line 1 upon the next iteration.
- a. Because this iteration colors z.p.p red, node $z'$ is red at the start of the next iteration.
- b. The node $z'.p$ is z.p.p.p in this iteration, and the color of this node does not change. If this node is the root, it was black prior to this iteration, and it remains black at the start of the next iteration.
- c. We have already argued that case 1 maintains property 5, and it does not introduce a violation of properties 1 or 3. If node $z'$ is the root at the start of the next iteration, the case 1 corrected the lone violation of property 4 in this iteration. Since $z'$ is red and it is the the root, property 2 becomes the only one that is violated, and this violation is due to $z'$. If node $z'$ is not the root at the start of the next iteration, then case 1 has not created a violation of property 2. Case 1 corrected the lone violation of property 4 that existed at the start of this iteration. It then made $z'$ red and left $z'$.p alone. If $z'$.p was black, there is no violation of property 4. If $z'$.p was red, coloring $z'$ red created one violation of property 4 between $z'$ and $z'$.p.
Figure 5 Case 1 of the procedure RB-INSERT-FIXUP. Property 4 is violated, since z and its parent z.p are both red. We take the same action whether (a) z is a right child or (b) z is a left child. Each of the subtree $\alpha$, $\beta$, $\gamma$, $\delta$, and $\varepsilon$ has a black root, and each has the same black-height. The code for case 1 change the colors of some nodes, preserving property 5: all downward simple paths from a node to a leaf have the same number of blacks. The while loop continues with node z's grandparent z.p.p as the new z. Any violation of property 4 can now occur only between the new z, which is red, and its parent, if it is red as well.
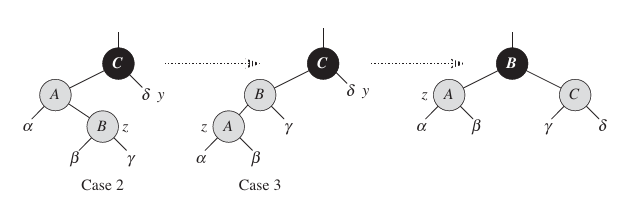
We now show that cases 2 and 3 maintain the loop invariant. (As we have just argued, z.p will be black upon the next test in line 1, and the loop body will not execute again.)
Case 2 makes z point to z.p, which is red. No further change to z or its color occurs in cases 2 and 3.
Case 3 makes z.p black, so that if z.p is the root at the start of the next iteration, it is black.
- As in case 1, properties 1, 3, and 5 are maintained in cases 2 and 3. Since node z is not the root in cases 2 and 3, we know that there is no violation of property 2. Cases 2 and 3 do not introduce a violation of property 2, since the only node that is made red becomes a child of a black node by the rotation in case 3. Case 2 and 3 correct the lone violation of property 4, and they do not introduce another violation.
Analysis
What is the runnint time of RB-INSERT? Since the height of a red-black tree on n nodes is O($log_2$n), lines 1-30 of RB-INSERT take O($log_2n$) time. In RB-INSERT-FIXUP, the while loop repeats only if case 1 occurs, and then the pointer z moves two levels up the tree. The total number of times the while loop can be executed is therefore O($log_2n$). Thus, RB-INSERT takes a total of O($log_2n$) time. Moreover, it never performs more than two rotations, since the while loop terminates if case 2 or case 3 is executed.
Deletion
Like the other basic operations on an n-node red-black tree, deletion of a node takes time O($log_2n$). Deleting a node from a red-black tree is a bit more complicated than inserting a node.
The procedure for deleting a node from a red-black tree is based on the TREE-DELETE procedure. First, we need to customize the TRANSPLANT subroutine that TREE-DELETE calls so that it applies to a red-black tree:
RB-TRANSPLANT(T, u, v)
if u.p == T.nil
T.root = v
elseif u == u.p.left
u.p.left = v
else u.p.right = v
v.p = u.p
The procedure RB-TRANSPLANT differs from TRANSPLANT in two ways. First, line 1 references the sentinel T.nil instead of NIL. Second, the assignment to v.p in line 6 occurs uncondictionally: we can assign to v.p even if v points to the sentinel. In fact, we shall exploit the ability to assign to v.p when v = T.nil.
The procedure RB-DELETE is like the TREE-DELETE procedure, but with additional lines of pseudocode. Some of the additional lines keep track of a node y that might cause violations of the red-black properties. When we want to delete node z and z has fewer than two children, then z is removed from the tree, and we want y to be z. When z has two children, then y should be z's successor, and y moves into z's position in the tree. We also remember y's color before it is removed from or moved within the tree, and we keep track of the node x that moves into y's original position in the tree, because node x might also cause violations of the red-black properties. After deleting node z, RB-DELETE calls an auxiliary procedure RB-DELETE-FIXUP, which changes colors and performs rotations to restore the red-black properties.
RB-DELETE(T, z)
y = z
y-original-color = y.color
if z.left == T.nil
x = z.right
RB-TRANSPLANT(T, z, z.right)
elseif z.right == T.nil
x = z.left
RB-TRANSPLANT(T, z, z.left)
else y = TREE-MINIMUM(z.right)
y-original-color = y.color
x = y.right
if y.p == z
x.p = y // x == T.nil
else RB-TRANSPLANT(T, y, y.right)
y.right = z.right
y.right.p = y
RB-TRANSPLANT(T, z, y)
y.left = z.left
y.left.p = y
y.color = z.color
if y-original-color == BLACK
RB-DELETE-FIXUP(T, x)
Although RB-DELETE contains almost twice as many lines of pseudocode as TREE-DELETE, the two procedures have the same basic structure. You can find each line of TREE-DELETE within RB-DELETE (with the changes of replacing NIL by T.nil and replacing calls to TRANSPLANT by calls to RB-TRANSPLANT), executed under the same conditions.
Here are the other differences between the two procedures:
- We maintain node y as the node either removed from the tree or moved within the tree. Line 1 sets y to point to node z when z has fewer than two children and is therefore removed. When z has two children, line 9 sets y to point to z's successor, just as in TREE-DELETE, and y will move into z's position in the tree.
Because node y's color might change, the variable y-original-color stores y's color before any changes occur, Line 2 and 10 set this variable immediately after assignments to y. When z has two children, then y != z and node y moves into node z's original position in the red-black tree; line 20 gives y the same color as z. We need to save y's original color in order to test it at the end of RB-DELETE; if it was black, then removing or moving y could cause violation of the red-black properties.
As discussed, we keep track of the node x that moves into node y's original position. The assignments in line 4, 7, and 11 set x to point to either y's only child or, if y has no children, the sentinel T.nil. (y has no left child.)
- Since node x moves into node y's original position, the attribute x.p is always set to point to the original position in the tree of y's parent, even if x is, in fact, the sentinel T.nil. Unless z is y's original parent (which occurs only when z has two children and its successor y is z's right child), the assignment to x.p takes place in line 6 of RB-TRANSPLANT. (Observe that when RB-TRANSPLANT is called in lines 5, 8, or 14, the second parameter passed is the same as x.).
When y's original parent is z, however, we do not want x.p to point to y's original parent, since we are removing that node from the tree. Because node y will move up to take z's position in the tree, setting x.p to y in line 13 cause x.p to point to the original position of y's parent, even if x == T.nil. Finally, if node y was black, we might have introduced one or more violations of the red-black properties, and so we call RB-DELETE-FIXUP in line 22 to restore the red-black properties. If y was red, the red-black properties still hold when y is removed or moved, for the following reasons:
- No black-heights in the tree have changed.
No red nodes have been made adjacent. Because y takes z's place in the tree, along with z's color, we cannot have two adjacent red nodes at y's new position in the tree. In addition, if y was not z's right child, then y's original right child x replaces y in the tree. If y is red, then x must be black, and so replacing y by x cannot cause two red nodes to become adjacent.
- Since y could not have been the root if it was red, the root remains black.
We can now see the procedure RB-DELETE-FIXUP and examine how it restores the red-black properties to the search tree.
RB-DELETE-FIXUP(T, x)
while x != T.root and x.color == BLACK
if x == x.p.left
w = x.p.right
if w.color == RED
w.color = BLACK // case 1
x.p.color = RED // case 1
LEFT-ROTATE(T, x.p) // case 1
w = x.p.right // case 1
if w.left.color == BLACK and w.right.color == BLACK
w.color = RED // case 2
x = x.p // case 2
else if w.right.color == BLACK
w.left.color = BLACK // case 3
w.color = RED // case 3
RIGHT-ROTATE(T, w) // case 3
w = x.p.right // case 3
w.color = x.p.color // case 4
x.p.color = BLACK // case 4
w.right.color = BLACK // case 4
LEFT-ROTATE(T, x.p) // case 4
x = T.root // case 4
else
w = x.p.left
if w.color == RED
w.color = BLACK // case 1
x.p.color = RED // case 1
RIGHT-ROTATE(T, x.p) // case 1
w = x.p.left // case 1
if w.right.color == BLACK and w.left.color == BLACK
w.color = RED // case 2
x = x.p // case 2
else if w.left.color == BLACK
w.right.color = BLACK // case 3
w.color = RED // case 3
LEFT-ROTATE(T, w) // case 3
w = x.p.left // case 3
w.color = x.p.color // case 4
x.p.color = BLACK // case 4
w.left.color = BLACK // case 4
RIGHT-ROTATE(T, x.p) // case 4
x = T.root // case 4
x.color = BLACK
- x points to a red-black node, in which case we color x (singly) black in line 23;
- x points to the root, in which case we simply "remove" the extra black: or
- having performed suitable rotations and recoloring, we exit the loop.
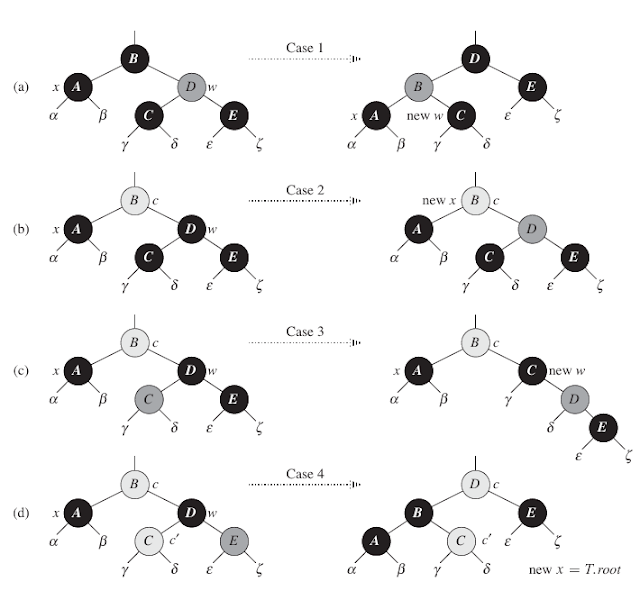
The four cases in the code appear in Figure 7. Before examining each case in detail, let's look more generally at how we can verify that the transformation in each of the cases preserves property 5. The key idea is that in each case, the transformation applied preserves the number of black nodes (including x's extra black) from (and including) the root of the subtree shown to each of the subtrees $\alpha$,$\beta$,...,$\zeta$. Thus, if property 5 holds prior to the transformation, it continues to hold afterward. For example, in Figure 7(a), which illustrates case 1, the number of black nodes from the root to either subtree $\alpha$ or $\beta$ is 3, both before and after the transformation. (Again, remember that node x adds an extra black.) Similarly, the number of black nodes from the root to any of $\gamma$, $\delta$, $\varepsilon$ and $\zeta$ is 2, both before and after the transformation. In Figure 7(b), the counting must involve the value c of the color attribute of the root of the subtree shown, which can be either RED or BLACK. If we define count(RED) = 0 and count(BLACK) = 1, then the number of black nodes from the root to $\alpha$ is 2 + count(c), both before and after the transformation. In this case, after the transformation, the new node x has color attribute c, but this ndoe is really either red-and-black (if c == RED) or doubly black (if c == BLACK). You can verify the other cases similarly.
Case 1: x's sibling w is red
Case 1 (lines 5-8 of RB-DELETE-FIXUP and Figure 7(a)) occurs when node w, the sibling of node x, is red. Since w must have black children, we can switch the colors of w and x.p and then perform a left-rotation on x.p without violating any of the red-black properties. The new sibling of x, which is one of w's children prior to the rotation, is now black, and thus we have converted case 1 into case 2, 3, or 4.
Case 2, 3 and 4 occur when node w is black; they are distinguished by the colors of w's children.
Case 2: x's sibling w is black, and both of w's children are black
In case 2 (lines 10-11 of RB-DELETE-FIXUP and Figure 7(b)), both of w's children are black. Since w is also black, we take one black off both x and w, leaving w with only one black and leaving w red. To compensate for removing one black from x and w, we would like to add an extra black to x.p, which was originally either red or black. We do so by repeating the while loop with x.p as the new node x. Observe that if we enter case 2 through case 1, the new ndoe x is red-and-black, since the original x.p was red. Hence, the value c of the color attribute of the new node x is RED, and the loop terminates when it tests the loop condition. We then color the new node x (singly) black in line 23.
Case 3: x's sibling w is black, w's left child is red, and w's right child is black
Case 3 (lines 13-16 and Figure 7(c)) occurs when w is black, its left child is red, and its right child is black. We can switch the colors of w and its left child w.left and then perform a right rotation on w without violating any of the red-black properties. The new sibling w of x is now a black node with a red right child, and thus we have transformed case 3 into case 4.
Case 4: x's sibling w is black, and w's right child is red
Case 4 (lines 17-21 and Figure 7(d)) occurs when node x's sibling w is black and w's right child is red. By making some color changes and performing a left rotation on x.p, we can remove the extra black on x, making it singly black, without violating any of the red-black properties. Setting x to be the root cause the while loop to terminate when ti tests the loop condition.
Analysis
What is the running time of RB-DELETE? Since the height of a red-black tree of n nodes is O($log_2n$), the total cost of the procedure without the call to RB-DELETE-FIXUP takes O($log_2n$) time. Within RB-DELETE-FIXUP, each of case 1, 3 and 4 lead to termination after performing a constant number of color changes and at most tree rotations. Case 2 is the only case in which the while loop can be repeated, and then the pointer x moves up the tree at most O($log_2n$) times, performing no rotations. Thus, the procedure RB-DELETE-FIXUP takes O($log_2n$) time and performs at most three rotations, and the overall time for RB-DELETE is therefore also O($log_2n$).
Figure 7 The cases in the while loop of the procedure RB-DELETE-FIXUP. Darkened nodes have color attributes BLACK, heavily shaded nodes have color attributes RED, and lightly shaded nodes have color attributes represented by c and $c'$, which may be either RED or BLACK. The letters $\alpha$,$\beta$,...,$\zeta$ represent arbitrary subtrees. Each transforms the configuration on the left into the configuration on the right by changing some colors and/or performing a rotation. Any node pointed to by x has an extra black and is either doubly black or red-and-black. Only case 2 causes the loop to repeat. (a) Case 1 is transformed to case 2, 3 or 4 by exchanging the color of nodes B and D and performing a left rotation. (b) In case 2, the extra black represented by the pointer x moves up the tree by coloring node D red adn setting x to point to node B. If we enter case through case 1, the while loop terminates because the new node x is red-and-black, and therefore the value c of its color attribute is RED. (c) Case 3 is transformed to case 4 by exchanging the colors of nodes C and D and performing a right rotation. (d) Case 4 removes the extra black represented by x by changing some colors and performing a left rotation (without violating the red-black properties), and then the loop terminates.
References:
Introduction to algorithms

Comments
Post a Comment