Software Developer

Install # pkg install zh-fcitx  # pkg install zh-fcitx-libpinyin # pkg install zh-fcitx-table-extra # pkg install zh-CJKUnifonts Configurations 1. 文件 ~/.cshrc 添加的內容如下: setenv XMODIFIERS @im=fcitx 2.文件 ~/.xinitrc 內容如下: exec fcitx -d & . /usr/local/etc/xdg/xfce4/xinitrc

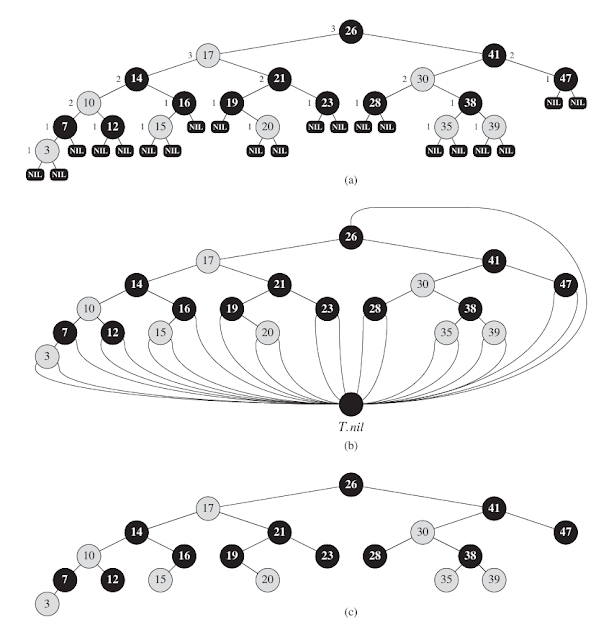
Binary Search Trees showed that a binary search tree of height h can support any of the basic dynamic-set operations—such as SEARCH, PREDECESSOR, SUCCESSOR, MINIMUM, MAXIMUM, INSERT, and DELETE—in O(h) time. Thus, the set operations are fast if the height of the search tree is small. If its height is large, however, the set operations may run no faster than with a linked list. Red-black trees are one of many search-tree schemes that are “balanced” in order to guarantee that basic dynamic-set operations take O($log_2n$) time in the worst case. Properties of red-black trees A red-black tree is a binary search tree with one extra bit of storage per node; its color , which can be either RED or BLACK. By constraining the node colors on any simple path from the root to a leaf, red-black trees ensure that no such path is more than twice as long as any other, so that the tree is approximately balanced . Each node of the tree now contains the attribute color , key , left , right , and p . I

What is a binary search tree? A binary search tree is organized, as the name suggests, in a binary tree,  as following:  Figure 1   Binary search trees. For any node x, the keys in the left subtree of x are at most x: key, and the keys in the right subtree of x are at least x: key. Different binary search trees can represent the same set of values. The worst-case running time for most search-tree operations is proportional to the height of the tree. (a) A binary search tree on 6 nodes with height 2. (b) A less efficient binary search tree with height 4 that contains the same keys. We can represent such a tree by a linked data structure in which each node is an object. In addition to a key and satellite data, each node contains attributes left , right and p that point to the nodes corresponding to its left child, its right child, and its parent, respectively. If a child or the parent is missing, the appropriate attribute contains the value NIL. The root node is the only node in the t

What is MathJax? Beautiful math in all browser - A JavaScript display engine for mathematics that works in all browsers. Add MathJax for Blogs on Blogger Layout -> SIdebar(bottom) [+ Add a Gadget] -> HTML/JavaScript Setting the Title as  "MathJax".   And add the below code to Content. <script type="text/x-mathjax-config"> //<![CDATA[ MathJax.Hub.Config({ tex2jax: { inlineMath: [ ['$','$'], ["\\(","\\)"] ], displayMath: [ ['$$','$$'], ["\\[","\\]"] ], processEscapes: true }, "HTML-CSS": { availableFonts: ["TeX"] } }); //]]> </script> <script async="async" src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.2/MathJax.js?config=TeX-AMS-MML_HTMLorMML" type="text/javascript"> </script>     Display Math Notations in Blog Posts Using the above setup, any math characters you

Layout -> SIdebar(bottom) [+ Add a Gadget] -> HTML/JavaScript Setting the Title as  "highlight". And add the below code to Content. <link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/highlight.js/11.3.1/styles/default.min.css" integrity="sha512-3xLMEigMNYLDJLAgaGlDSxpGykyb+nQnJBzbkQy2a0gyVKL2ZpNOPIj1rD8IPFaJbwAgId/atho1+LBpWu5DhA==" crossorigin="anonymous" referrerpolicy="no-referrer" /> <script src="https://cdnjs.cloudflare.com/ajax/libs/highlight.js/11.3.1/highlight.min.js" integrity="sha512-Pbb8o120v5/hN/a6LjF4N4Lxou+xYZ0QcVF8J6TWhBbHmctQWd8O6xTDmHpE/91OjPzCk4JRoiJsexHYg4SotQ==" crossorigin="anonymous" referrerpolicy="no-referrer"></script> <script src="//cdnjs.cloudflare.com/ajax/libs/highlightjs-line-numbers.js/2.8.0/highlightjs-line-numbers.min.js"></script> <script>hljs.highlightAll();hljs.initLineNumbersOnLo

Definitions In computer science, a binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child . Properties 1. The maximum number of nodes at level $i$ of a binary tree is $2^{i-1} (i \geqslant 1)$ or $2^i(i \geqslant 0)$. Here level is the number of nodes on the path from the root to the node (including root and node). Level of the root is 1. Proof:   Let,  the maximum number of nodes on level i is S(i) = $2^{i-1}$           S(1) = $2^{1-1}$ = $2^0$ = 1 (By substituting $i$ = 1 on both sides)          $\therefore$ S(1) is true. Let, S(i) be true for some natural number k. i.e., S(k) = $2^{k-1}$   Now,           Since in Binary tree every node has at most 2 children, next level (k+1) would have twice nodes. i.e., S(k+1) = 2* S(k) = 2 * $2^{k-1}$ = $2^{(k-1)+1}$ = $2^k$ = $2^{(k+1)-1}$     $\Longrightarrow$  S(k+1) is true. Hence by principle of mathematical induction, the maximum number of nodes at lev